Zeno of Elea (Ζήνων ὁ Ἐλεάτης) lived from around 490 BC to 430 BC. He was a pre-Socratic Hellenic philosopher of Magna Graecia (the name given by the Romans to the coastal areas of Southern Italy) and a member of the Eleatic School founded by Parmenides. He is best known for a series of paradoxes which have puzzled, challenged, influenced, inspired, infuriated, and amused philosophers, mathematicians, and physicists for over two millennia. Perhaps the famoust of the paradoxes is the Achilles Paradox.
This is the paradox: Achilles, who we can assume is the fastest runner of antiquity, is racing to catch the tortoise that is slowly crawling away from him. Both are moving along a linear path at constant speeds. In order to catch the tortoise, Achilles will have to reach the place where the tortoise presently is. However, by the time Achilles gets there, the tortoise will have crawled to a new location. Achilles will then have to reach this new location. By the time Achilles reaches that location, the tortoise will have moved on to yet another location, and so on forever. Zeno claims Achilles will never catch the tortoise. Confused? Perhaps a video will help.
Although practically no scholars today would agree with Zeno’s conclusion, we cannot escape the paradox. Zeno assumed distances and durations can be endlessly divided into parts, and he assumed there are too many of these parts for the runner to complete. With this, he emphasized the distinction between appearance and reality; it would appear that Achilles would blow past the tortoise in a few paces but in reality there are an infinite number of points Achilles must reach where the tortoise has already been, he can never overtake the tortoise. The paradox thus supports his teacher Parmenides' doctrine that contrary to the evidence of one's senses, the belief in plurality and change is mistaken, and in particular that motion is nothing but an illusion.
The source for Zeno's views is Aristotle (Physics Book VI, Chapter 8, 239b14-16) and some passages from Simplicius in the fifth century C.E. There is no evidence that Zeno used a tortoise rather than a slow human. The tortoise is a later commentator’s addition. Aristotle spoke simply of “the runner” who competes with Achilles.
So how do we solve the paradox instead of rejecting it? It boils down to the following 'problem': the tortoise moves continuous but because Achilles has to catch up, his path is discrete; he is, after all, continually catching up to a set point in space where the tortoise no longer is. This would look something like this:
- - - - - - - - - - - - -
Achilles' discrete path
It's too easy to say that if Achilles' aim is to overtake the turtoise, he should aim for a point ahead of the turtoise and thus create a continual path; if he did he is still required to go to every one of those locations that the tortoise touched. So what is the solution? It took humanity a while but we've come up with a Standard Solution to all of Zeno's paradoxes having to do with motion: math. First we must break down the paradox:
1: Achilles must first traverse an infinite number of divisions in order to reach the tortoise
2: it is impossible for Achilles to traverse an infinite number of divisions
3: therefore, Achilles can never surpass the tortoise
To overcome the paradox, one must prove mathamathically that Achilles isn't, in fact, following a discrete path but a continuum of his own. If they move move at a continuum, Achilles would very quickly overtake the turtoise, after all.
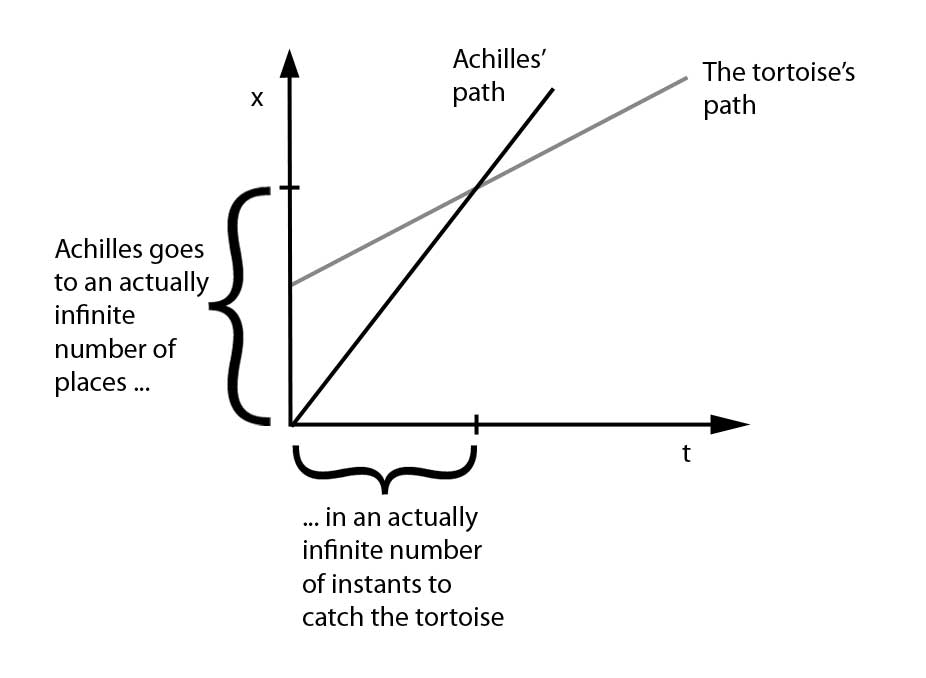
The math: Achilles travels a distance d1 in reaching the point x1 where the tortoise starts, but by the time Achilles reaches x1, the tortoise has moved on to a new point x2. When Achilles reaches x2, having gone an additional distance d2, the tortoise has moved on to point x3, requiring Achilles to cover an additional distance d3, and so forth. This sequence of non-overlapping distances (or intervals or sub-paths) is an actual infinity, but happily the geometric series converges. The sum of its terms d1 + d2 + d3 +… is a finite distance that Achilles can readily complete while moving at a constant speed. Here, have a chart:
The Achilles Argument presumes that space and time are continuous or infinitely divisible. So, Zeno's conclusion may not simply have been that Achilles cannot catch the tortoise but instead that he cannot catch the tortoise if space and time are infinitely divisible. Whatever the case, it's taken millenia to even come up with a standerd to beat the paradox--and that means that as ludicrous as the paradox sounds, it is definitely intricate and very advanced.
This is the paradox: Achilles, who we can assume is the fastest runner of antiquity, is racing to catch the tortoise that is slowly crawling away from him. Both are moving along a linear path at constant speeds. In order to catch the tortoise, Achilles will have to reach the place where the tortoise presently is. However, by the time Achilles gets there, the tortoise will have crawled to a new location. Achilles will then have to reach this new location. By the time Achilles reaches that location, the tortoise will have moved on to yet another location, and so on forever. Zeno claims Achilles will never catch the tortoise. Confused? Perhaps a video will help.
Although practically no scholars today would agree with Zeno’s conclusion, we cannot escape the paradox. Zeno assumed distances and durations can be endlessly divided into parts, and he assumed there are too many of these parts for the runner to complete. With this, he emphasized the distinction between appearance and reality; it would appear that Achilles would blow past the tortoise in a few paces but in reality there are an infinite number of points Achilles must reach where the tortoise has already been, he can never overtake the tortoise. The paradox thus supports his teacher Parmenides' doctrine that contrary to the evidence of one's senses, the belief in plurality and change is mistaken, and in particular that motion is nothing but an illusion.
The source for Zeno's views is Aristotle (Physics Book VI, Chapter 8, 239b14-16) and some passages from Simplicius in the fifth century C.E. There is no evidence that Zeno used a tortoise rather than a slow human. The tortoise is a later commentator’s addition. Aristotle spoke simply of “the runner” who competes with Achilles.
So how do we solve the paradox instead of rejecting it? It boils down to the following 'problem': the tortoise moves continuous but because Achilles has to catch up, his path is discrete; he is, after all, continually catching up to a set point in space where the tortoise no longer is. This would look something like this:
________________________
The tortoise' continual path
The tortoise' continual path
- - - - - - - - - - - - -
Achilles' discrete path
It's too easy to say that if Achilles' aim is to overtake the turtoise, he should aim for a point ahead of the turtoise and thus create a continual path; if he did he is still required to go to every one of those locations that the tortoise touched. So what is the solution? It took humanity a while but we've come up with a Standard Solution to all of Zeno's paradoxes having to do with motion: math. First we must break down the paradox:
1: Achilles must first traverse an infinite number of divisions in order to reach the tortoise
2: it is impossible for Achilles to traverse an infinite number of divisions
3: therefore, Achilles can never surpass the tortoise
To overcome the paradox, one must prove mathamathically that Achilles isn't, in fact, following a discrete path but a continuum of his own. If they move move at a continuum, Achilles would very quickly overtake the turtoise, after all.
The math: Achilles travels a distance d1 in reaching the point x1 where the tortoise starts, but by the time Achilles reaches x1, the tortoise has moved on to a new point x2. When Achilles reaches x2, having gone an additional distance d2, the tortoise has moved on to point x3, requiring Achilles to cover an additional distance d3, and so forth. This sequence of non-overlapping distances (or intervals or sub-paths) is an actual infinity, but happily the geometric series converges. The sum of its terms d1 + d2 + d3 +… is a finite distance that Achilles can readily complete while moving at a constant speed. Here, have a chart:
No comments:
Post a Comment